Media aritmético-geométrica

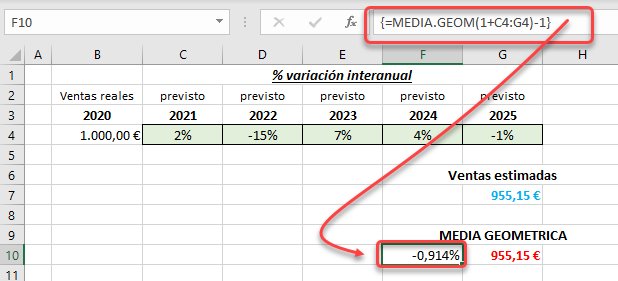
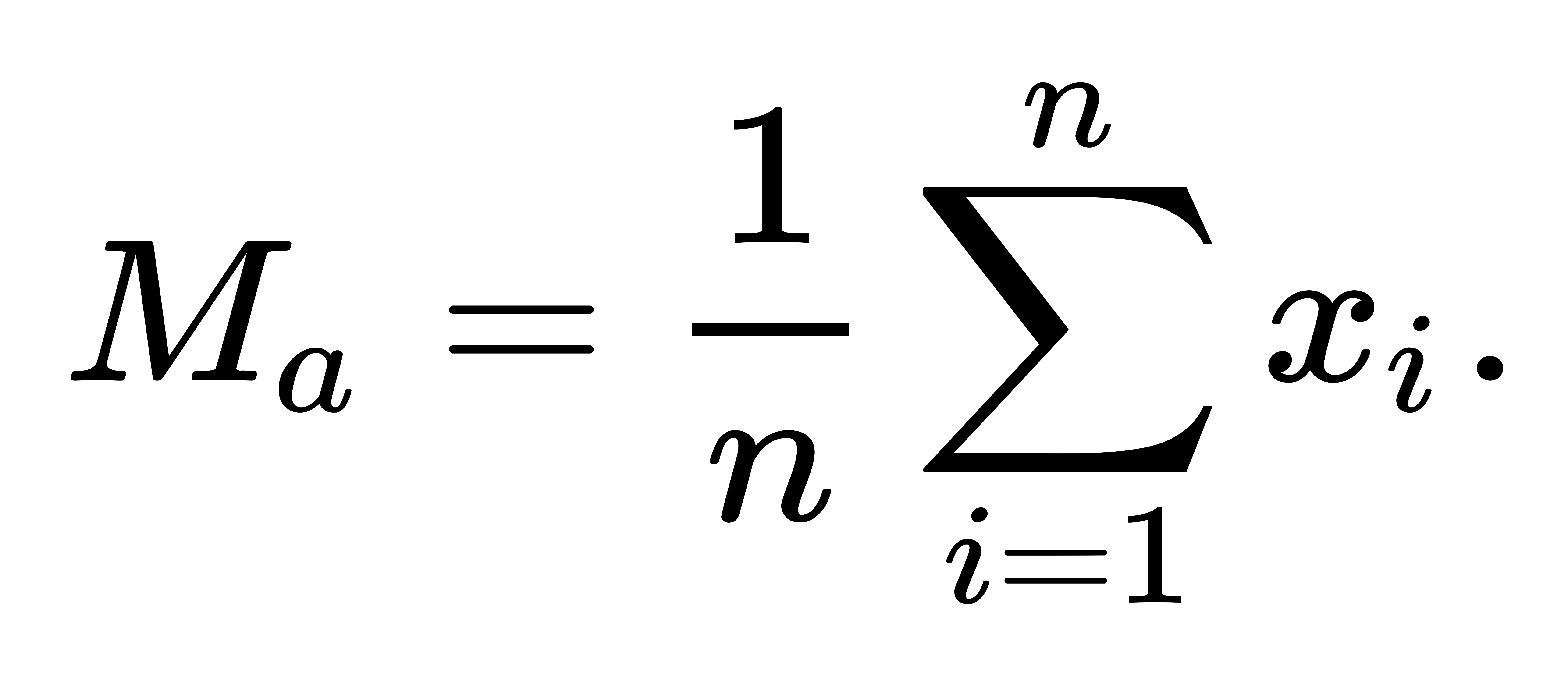La media aritmético-geométrica M(x, y) de dos números reales positivos x e y se define de la siguiente forma:

• Primero, se obtiene la media aritmética de x e y denominándola a₁, i.e. a₁ = (x y) / 2.
• Después se calcula la media geométrica de x e y denominándola g₁, i.e. g₁ es la raíz cuadrada de xy.
• A continuación, se itera esta operación con a₁ en lugar de x y g₁ en lugar de y. De esta forma, se definen dos sucesiones (a_n) y (g_n):

${\displaystyle a_{n 1}={\frac {a_{n} g_{n}}{2}}\quad {\mbox{y}}\quad g_{n 1}={\sqrt {a_{n}g_{n}}}}$

Ambas sucesiones convergen al mismo número, denominado media aritmético-geométrica M(x, y) de x e y.

Origen Algebraico de la Media Aritmético - Geométrica

https://web.archive.org/web/20160818061731/http://www.cerano.com.mx/cerano_v2/media-aritmetico-geometrica/

Propiedades

Se puede demostrar además que:

${\displaystyle M(x,y)={\frac {\pi }{4}}\cdot {\frac {x y}{K\left({\frac {x-y}{x y}}\right)}}}$

donde K(x) es la integral elíptica completa de primera especie. Otra identidad interesante en la que interviene la media aritmética geométrica es la siguiente:

${\displaystyle {\frac {1}{M(a,b)}}={\frac {2}{\pi }}\int _{0}^{\pi /2}{\frac {d\theta }{\sqrt {a^{2}\cos ^{2}\theta b^{2}\sin ^{2}\theta }}}={\frac {1}{\pi }}\int _{-\infty }^{\infty }{\frac {dt}{\sqrt {(a^{2} t^{2})(b^{2} t^{2})}}}}$

Véase también

• Media generalizada
• Desigualdad de las medias aritmética y geométrica
• Algoritmo de Gauss-Legendre

Enlaces externos

• Hazewinkel, Michiel, ed. (2001), «Media aritmético-geométrica», Encyclopaedia of Mathematics (en inglés), Springer, ISBN 978-1556080104 .
• Weisstein, Eric W. «Arithmetic–Geometric mean». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.